.....................Movimiento ...............................Ondulatorio..................: septiembre 2010

viernes, 17 de septiembre de 2010

Un sobretono es un componente senosoidal de la forma de una onda, de mayor frecuencia que su frecuencia fundamental. Generalmente el primer sobretono es el segundo armónico, el segundo sobretono el tercer armónico, etcétera.

Típicamente el término se refiere a ondas acústicas, especialmente en cuanto a temas relacionados a la música. A pesar del uso mezclado, un sobretono o es armónico o es parcial. El sobretono parcial o inarmónico es un múltiplo no entero de una frecuencia fundamental.

Un ejemplo de sobretonos armónicos: “Sobretonos armónicos”.

f	440 Hz	tono fundamental	primer armónico
2f	880 Hz	primer sobretono	segundo armónico
3f	1320 Hz	segundo sobretono	tercer armónico

No todos los sobretonos son armónicos, o múltiplos enteros de la frecuencia fundamental. Algunos instrumentos musicales producen sobretonos más agudos o encerrados que los armónicos. Esta característica es uno de los varios elementos que aportan a su sonido.; como efecto secundario hace que las formas de onda no sean completamente periódicas.

La fundamental es la frecuencia a la que vibra la onda completa. Los sobretonos son otros componentes sinusoides presentes a frecuencias superiores a la fundamental. Todos los componentes de frecuencia que forman la forma de onda completa, incluyendo el fundamental y los sobretonos se llaman parciales.

Los sobretonos que son múltiplos enteros del fundamental se llaman armónicos. Cuando un sobretono está cerca de ser armónico, a menudo se llama armónico parcial, aunque se denomina simplemente como armónico. Algunas veces los sobretonos no están cerca de ningún armónico, entonces se llaman parciales o sobretonos inarmónicos.

La frecuencia fundamental se considera el primer armónico y el primer parcial. La numeración de los parciales y armónicos es normalmente la misma, el segundo parcial es el segundo armónico, etc. Pero si hay parciales inarmónicos, la numeración no coincidirá. Los sobretonos, están numerados según estén por encima del fundamental. Hablando estrictamente, el primer sobretono es el segundo parcial (y normalmente el segundo armónico). Como esto puede resultar confuso, sólo los armónicos se llaman por sus números y los sobretonos y los parciales se describen según su relación con estos armónicos.

Cuando una onda periódica está compuesta de un fundamental y sólo armónicos impares (f, 3f, 5f, 7f,...), la onda suma es una media onda simétrica, es decir, se puede invertir y cambiar la fase y sería exactamente la misma. Si la onda tiene algún armónico par (0f, 2f, 4f, 6f,...) será asimétrica, la parte de arriba no será una imagen especular de la de abajo.

El contrario también es cierto. Un sistema que cambia la forma de la onda (mediante escalado o desplazamiento de fase) crea armónicos adicionales (distorsión armónica) y se dice que es un sistema no lineal. Si afecta a la onda simétricamente, los armónicos producidos sólo serán impares, si la afecta asimétricamente, habrá al menos un armónico par.

NODOS Y ANTINODOS

En física, el nodo es todo punto de una onda estacionaria cuya amplitud es cero en cualquier momento.

El punto intermedio de cada par de nodos, la amplitud de vibración máxima se denomina vientre o antinodo.

Hay puntos que no vibran (nodos), que permanecen inmóviles, estacionarios, mientras que otros (vientres o antinodos) lo hacen con una amplitud de vibración máxima, igual al doble de la de las ondas que interfieren, y con una energía máxima. El nombre de onda estacionaria proviene de la aparente inmovilidad de los nodos. La distancia que separa dos nodos o dos antinodos consecutivos es media longitud de onda.

Si las ondas armónicas se combinan en determinado medio y tienen la misma frecuencia y longitud de onda, se encuentra que la resultante posee un patrón estacionario, denominado onda estacionaria.

Para entender mejor los que son los “nodos y antinodos” veremos lo siguiente:

Onda estacionaria:

Un tipo de superposición de ondas especialmente interesante es el que tiene lugar entre dos ondas de idénticas características pero propagándose en sentido contrario. Las ondas resultantes reciben el nombre de ondas estacionarias, pues no implican un movimiento de avance de la perturbación.

Este tipo de ondas están asociadas a reflexiones en los límites de separación de medios de propiedades diferentes. Dichos límites pueden ser básicamente de dos tipos, libres y fijos. El nudo de unión de dos cuerdas de diferente grosor sería un ejemplo de límite libre; por el contrario, el extremo de la cuerda unido a un punto fijo en una pared sería un límite fijo.

Se comprueba experimentalmente que en un límite libre la onda reflejada tiene las mismas características que la onda incidente, tan sólo difieren en el sentido de avance de la perturbación. Por el contrario, en un límite fijo la onda reflejada posee las mismas características que la incidente, pero está desfasada p radianes respecto a la onda incidente.

Consideremos en primer lugar las ondas estacionarias (que se propagan en el eje x) por reflexión en un límite libre. La función de onda resultante será:

Recordando que

se tiene

Esta no es la ecuación de una onda que se propaga, sino de un movimiento armónico simple (estacionario) cuya amplitud ( 2A cos kx ) varía de un punto a otro del espacio. La perturbación no se propaga a lo largo del eje X.

Los puntos de máxima amplitud (±2A ) se llaman vientres o antinodos. En ellos se debe cumplir:

Los puntos de mínima amplitud (nula) se llaman nodos. En ellos se debe cumplir:

Así pues, tanto los nodos como los vientres aparecen a intervalos de longitud l/2, mediando entre un nodo y un antinodo una distancia de l/4.

Imágenes en dos instantes de la onda estacionaria producida por reflexión en un límite libre, los nodos se representan como N y los antinodos como A

Consideremos ahora las ondas estacionarias por reflexión en un límite fijo. La función de onda resultante será:

Recordando que

se tiene

Como antes, esta no es la ecuación de una onda, sino de un movimiento armónico simple cuya amplitud ( 2A sen kx ) varía de un punto a otro del espacio. La perturbación no se propaga a lo largo del eje X.

Los vientres estarán dados por:

Y los nodos por:

Así pues, tanto los nodos como los vientres aparecen a intervalos de longitud l/2, mediando entre un nodo y un antinodo una distancia de l/4.

Dos imágenes superpuestas de una onda estacionaria (en dos instantes de tiempo) producida por reflexión en un límite fijo, los nodos se representan como N y los antinodos como A

Si el medio está limitado por sus dos extremos fijos, una vez que la perturbación se produce en él se automantiene por reflexiones sucesivas en los límites dando lugar a una onda estacionaria.

Nodos y antinodos

Los palos de la clave, tanto como las láminas de un xylofón o una marimba, cuando se golpean producen una vibración perpendicularmente en sentido longitudinal transversal. En un palo se forman nodos y antinodos.

Los antinodos son los puntos de amplitud de vibración máxima. Los nodos son los puntos donde la vibración tiene un valor nulo. Cada palo de la clave tiene tres antinodos y dos nodos. Los antinodos se encuentran en el centro y en los extremos, nos nodos se encuentran intercalados. Por la forma perfectamente cilíndrica, la percusión se produce en un solo punto.

Para hacer vibrar un palo hay que golpearlo en un punto donde se encuentra un antinodo. Generalmente se golpea en el centro. En el caso de la clave se golpea con el macho la hembra en su centro. Para obtener más calidad del sonido (penetrante y agudo) se golpea la hembra con esta parte del macho donde hay un nodo. Entonces el sonido será lleno. Si se golpea la hembra con los extremos o con el centro del macho entonces el macho mismo entra en vibración por lo que las vibraciones de ambos palos parecen extinguéndose mutuamente. Entonces el sonido es apagado.

Frecuencias caracteristicas

Frecuencia absoluta:

La frecuencia absoluta de una variable estadística es el número de veces que aparece en la muestra dicho valor de la variable, la representaremos por n_i

Frecuencia relativa:

La frecuencia absoluta, es una medida que está influida por el tamaño de la muestra, al aumentar el tamaño de la muestra aumentará también el tamaño de la frecuencia absoluta. Esto hace que no sea una medida útil para poder comparar. Para esto es necesario introducir el concepto de frecuencia relativa, que es el cociente entre la frecuencia absoluta y el tamaño de la muestra. La denotaremos por f_i

Donde N = Tamaño de la muestra

Porcentaje:

La frecuencia relativa es un tanto por uno, sin embargo, hoy día es bastante frecuente hablar siempre en términos de tantos por ciento o porcentajes, por lo que esta medida resulta de multiplicar la frecuencia relativa por 100. La denotaremos por p_i.

Frecuencia Absoluta Acunulada:

Para poder calcular este tipo de frecuencias hay que tener en cuenta que la variable estadística ha de ser cuantitativa o cualitativa ordenable. En otro caso no tiene mucho sentido el cálculo de esta frecuencia. La frecuencia absoluta acumulada de un valor de la variable, es el número de veces que ha aparecido en la muestra un valor menor o igual que el de la variable y lo representaremos por N_i.

&NBSP;
&NBSP;

Frecuencia Relativa Acunulada:

Al igual que en el caso anterior la frecuencia relativa acumulada es la frecuencia absoluta acumulada dividido por el tamaño de la muestra, y la denotaremos por F_i

Ondas estacionarias

Una onda estacionaria se forma por la interferencia de dos ondas de la misma naturaleza con igualamplitud, longitud de onda (o frecuencia) que avanzan en sentido opuesto a través de un medio.

Las ondas estacionarias permanecen confinadas en un espacio (cuerda, tubo con aire, membrana, etc.). La amplitud de la oscilación para cada punto depende de su posición, la frecuencia es la misma para todos y coincide con la de las ondas que interfieren. Hay puntos que no vibran (nodos), que permanecen inmóviles, estacionarios, mientras que otros (vientres o antinodos) lo hacen con una amplitud de vibración máxima, igual al doble de la de las ondas que interfieren, y con una energía máxima. El nombre de onda estacionaria proviene de la aparente inmovilidad de los nodos. La distancia que separa dos nodos o dos antinodos consecutivos es media longitud de onda.

Se puede considerar que las ondas estacionarias no son ondas de propagación sino los distintos modos de vibración de la cuerda, el tubo con aire, la membrana, etc. Para una cuerda, tubo, membrana, ... determinados, sólo hay ciertas frecuencias a las que se producen ondas estacionarias que se llaman frecuencias de resonancia. La más baja se denomina frecuencia fundamental, y las demás son múltiplos enteros de ella (doble, triple, ...).

Onda Completa

Se considera que una onda es completa cuando ha finalizado su recorrido, lo que podemos considerar como dos movimientos;

Cuando llega a una cresta consecutiva, habiendo recorrido un valle.
Viceversa.

Se pueden obtener por la suma de dos ondas atendiendo a la formula:

$\displaystyle y_1=A(\sin (kx + \omega t))$

$\displaystyle y_2=A(\sin (kx - \omega t))$

$\displaystyle y = y_1 + y_2 = A(\sin (kx + \omega t) + \sin (kx - \omega t))$

Siendo para x=0 y t=0 entonces y=0, para otro caso se tiene que añadir su correspondiente ángulo de desfase.

Estas formula nos da como resultado:

$y(x,t)= 2A \sin (kx) \cdot \cos{(\omega t)}$

Siendo $k = \frac{2 \pi}{\lambda} \,$ y $\omega = 2 \pi f = \frac{2 \pi}{T} \,$

[editar] Vientres y nodos

Se produce un vientre cuando $\displaystyle \sin (kx)= + 1 \text{ó} - 1 , \text{siendo } kx= \frac{\pi}{2} , \frac{3\pi}{2},...,\frac{(2n+1)\pi}{2} \text{ para } \forall n \in \mathbb{Z}$

$\text{Si }k = \frac{2 \pi}{\lambda} \, \text{ entonces } x=\left(n + \frac{1}{2}\right) \cdot \frac{\lambda}{2} \qquad \text{para } \forall n \in \mathbb{Z}$

Se produce un nodo cuando $\displaystyle \sin (kx)=$ $\displaystyle 0 , \text{siendo } \displaystyle kx=0,\pi,...,n\pi\text{ para } \forall n \in \mathbb{Z}$

$\text{Si }k = \frac{2 \pi}{\lambda} \, \text{ entonces }x= n \cdot \frac{\lambda}{2} \qquad \text{para } \forall n \in \mathbb{Z}$

Siendo

λ

la longitud de la onda.

[editar] Ondas estacionarias en una cuerda

Frecuencias fundamentales.

La frecuencia más baja para la que se observan ondas estacionarias en una cuerda de longitud L es la que corresponde a n = 1 en la ecuación de los nodos, que representa la distancia máxima posible entre dos nodos de una longitud dada. Ésta se denomina frecuencia fundamental, y cuando la cuerda vibra de este modo no se presentan nodos intermedios entre sus dos extremos. La siguiente posibilidad en la ecuación, el caso n = 2, se llama segundo armónico, y presenta un nodo intermedio.

$\text{Si } x=L \text{ y } \lambda = \lambda_n \text{ entonces } L= n \cdot \frac{\lambda_n}{2} \qquad \text{ siendo } L \text{ la longitud de la cuerda dada}$

despejamos

λ n

$\lambda_n = \frac{2L}{n}$

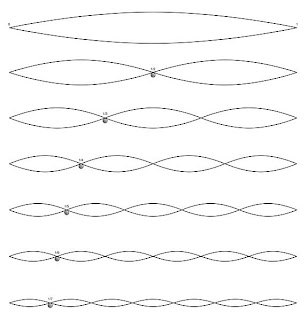
Ondas estacionarias en una cuerda

Frecuencias fundamentales.

Ondas estacionarias en líneas de transmisión de ondas de radio

En transmisión de ondas de radio, las ondas estacionarias en las líneas de transmisión son sumamente peligrosas para la integridad física de los componentes. Un aparato, el ROE-metro, mide el porcentaje de la onda incidente que es reflejada.

En el caso ideal en que se estableciera una onda estacionaria en la línea de transmisión, el transmisor terminaría por destruirse.

Una ROE (Relación de Onda Estacionaria) de 1,5 equivale a una reflexión de 4% de la onda incidente, y se admite que es el máximo que un transmisor de 100 Watts a transistores puede soportar sin sufrir daños. En cambio, los transmisores a válvulas son menos sensibles a las ondas estacionarias.

Ondas sonoras estacionarias

Es un fenómeno relacionado con la reflexión del sonido. Dependiendo de cómo coincidan las fases de la onda incidente y de la reflejada, se producirán modificaciones del sonido (aumenta la amplitud o disminuye), por lo que el sonido resultante puede resultar desagradable.

Cuando la longitud de la onda estacionaria es igual a una de las dimensiones de una sala (largo, alto o ancho), se dice que la sala está en resonancia. El efecto es aún más desagradable si cabe. Hay puntos donde no llega ningún sonido (interferencia destructiva) y otros donde la amplitud se dobla (interferencia constructiva). Gráficamente, si se viese la onda se vería que la sinusoide ha desaparecido y la onda ha adquirido forma de dientes de sierra. La ondas estacionarias también se llaman eigentonos omodos de la sala.

Principio de Superposicion

El principio de superposición o teorema de superposición es un resultado matemático que permite descomponer un problema lineal en dos o más subproblemas más sencillos, de tal manera que el problema original se obtiene como "superposición" o "suma" de estos subproblemas más sencillos.

Técnicamente, el principio de superposición afirma que cuando las ecuaciones de comportamiento que rigen un problema físico son lineales, entonces el resultado de una medida o la solución de un problema práctico relacionado con una magnitud extensiva asociada al fenómeno, cuando están presentes los conjuntos de factores causantes A y B, puede obtenerse como la suma de los efectos de A más los efectos de B.

Las ecuaciones de equilibrio de un sólido resistente que relacionan las fuerzas exteriores sobre un sólido con las tensiones internas son lineales; eso significa que para cualquier sólido que no plastifique, si se duplica en valor de las fuerzas se duplicará el valor de las tensiones.

Eso sucede con independencia de la ecuación constititutiva del material, sea éste o no elástico, siempre y cuando el estado final no dependa del modo de aplicación de las cargas. En problemas de plasticidad esta condición no se cumple en general, ya que el estado final depende de la "trayectoria" que siga el estado tensional; es decir, del modo, orden y velocidad con la que se aplican las cargas.

Energia de las ondas periodicas

Las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:

$x_a (t) = x_a (t+T_p) = x_a (t+nT_p) \,\!$

donde el periodo propio fundamental $T_p = \frac {1}{F} \,\!$ , $F \,\!$ es la frecuencia de la componente fundamental de la onda periódica y $n \,\!$ un número entero.

Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático).

La forma más simple de onda periódica es la onda armónica (sinusoidal), que se describe matemáticamente:

$x_a (t) = A \sin (\Omega t + \theta) \,\!$

La energía mecánica de un elemento dx de cuerda no se conserva. El elemento cuyo centro de masa está instantáneamente en la posición de equilibrio, tiene máxima deformación y máxima rapidez, por tanto tendrá máxima energía potencial y máxima energía cinética. El elemento cuyo centro de masa está instantáneamente en una cresta o en un valle, tendrá pendiente cero (no está deformado) y rapidez cero, por tanto tendrá energía potencial nula y energía cinética nula. En definitiva no hay conversión de energía cinética en potencial y viceversa. Podría pensarse como un caso de violación de la conservación de la energía, sin embargo, la energía mecánica no permanece constante es debido a que la energía está fluyendo (se está propagando).

En la siguiente simulación se ilustra la variación de las energías cinética, potencial y mecánica de todos los elementos de una cuerda por la que se propaga una onda transversal. Se detalla la variación de estas energías en uno de los elementos.

Fecuencia

Frecuencia es una medida que se utiliza generalmente para indicar el número de repeticiones de cualquier fenómeno o suceso periódico en la unidad de tiempo.

Ejemplos de ondas de distintas frecuencias; se observa la relación inversa con la longitud de onda.

Para calcular la frecuencia de un suceso. Según el SI (Sistema Internacional), la frecuencia se mide en hercios Heinrich Rudolf Hertz. Un hercio es aquel suceso o fenómeno repetido una vez por segundo. Así, dos hercios son dos sucesos (períodos) por segundo, etc. Esta unidad se llamó originariamente «ciclo por segundo» (cps) y aún se sigue utilizando. Otras unidades para indicar la frecuencia son revoluciones por minuto (rpm) y radianes por segundo (rad/s). Las pulsaciones del corazón y el tempo musical se mide en «pulsos por minuto» (bpm, del inglés beats per minute). (Hz), en honor a

$1 \,\mathrm{Hz} = \frac{1}{\mathrm{s}}$

Un método alternativo para calcular la frecuencia es medir el tiempo entre dos repeticiones (periodo) y luego calcular la frecuencia (f) recíproca de esta manera:

$f = \frac{1}{T}$

donde T es el periodo de la señal.

.....................Movimiento ...............................Ondulatorio..................