Las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:

donde el periodo propio fundamental 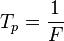 ,
,  es la frecuencia de la componente fundamental de la onda periódica y
es la frecuencia de la componente fundamental de la onda periódica y  un número entero.
un número entero.
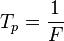 ,
,  es la frecuencia de la componente fundamental de la onda periódica y
es la frecuencia de la componente fundamental de la onda periódica y  un número entero.
un número entero.Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático).
La forma más simple de onda periódica es la onda armónica (sinusoidal), que se describe matemáticamente:

La energía mecánica de un elemento dx de cuerda no se conserva. El elemento cuyo centro de masa está instantáneamente en la posición de equilibrio, tiene máxima deformación y máxima rapidez, por tanto tendrá máxima energía potencial y máxima energía cinética. El elemento cuyo centro de masa está instantáneamente en una cresta o en un valle, tendrá pendiente cero (no está deformado) y rapidez cero, por tanto tendrá energía potencial nula y energía cinética nula. En definitiva no hay conversión de energía cinética en potencial y viceversa. Podría pensarse como un caso de violación de la conservación de la energía, sin embargo, la energía mecánica no permanece constante es debido a que la energía está fluyendo (se está propagando).

4 comentarios:
LA ENERGÍA SE CREA:
Una chispa salta desde un conductor, produciendo una vibración en el campo electromagnético y generando una radiación electromagnética, y su frente de onda esférico instantáneamente se acelera a la velocidad de la luz y crece como un globo que se infla y esa esfera puede llegar a ser de los objetos más grandes del universo y atraviesa el cosmos reproduciéndose en la distancia y en el tiempo…
Solo los dogmáticos y sectarios enceguecidos por un paradigma pueden afirmar que LA ENERGÍA NO SE CREA.
Los dogmáticos son tan absurdos y peligrosos que han llegado hasta el extremo de quemar vivos a sus contradictores. HOY BORRAN LOS COMENTARIOS.
ES HORA DE CONOCER EL OTRO 96% OSCURO DEL UNIVERSO.
Si quieres conocer la nueva "Teoría sobre el Universo" solicítala gratuitamente a: martinjaramilloperez@gmail.com
Pinshi Fondo Nos Cago La Tarea x 2 ijopta
EL GENERADOR PIEZOELÉCTRICO DE PASCAL también demuestra que el principio de conservación de la energía no es válido porque cea energía. El principio de Pascal multiplica la energía de presión intermitente y la piezoelectricidad transforma esa energía de presión multiplicada en electricidad. El Principio de Pascal actuando sobre grandes superficies piezoeléctricas crea energía.
El PRINCIPIO DE PASCAL MULTIPLICA LA PRESIÓN Y LA PIEZOELECTRICIDAD CONVIERTE LA PRESIÓN EN ELECTRICIDAD, Los dos fenómenos juntos contradicen el PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA porque multiplican la energía, crean energía, como lo demuestra el innovador GENERADOR PIEZOELECTRICO DE PASCAL. Las patentes internacionales del nuevo generador serán de propiedad colectiva de los usuarios de la energía, si quiere participar contacte a: martinjaramilloperez@gmail.com
Publicar un comentario