Una onda estacionaria se forma por la interferencia de dos ondas de la misma naturaleza con igualamplitud, longitud de onda (o frecuencia) que avanzan en sentido opuesto a través de un medio.
Las ondas estacionarias permanecen confinadas en un espacio (cuerda, tubo con aire, membrana, etc.). La amplitud de la oscilación para cada punto depende de su posición, la frecuencia es la misma para todos y coincide con la de las ondas que interfieren. Hay puntos que no vibran (nodos), que permanecen inmóviles, estacionarios, mientras que otros (vientres o antinodos) lo hacen con una amplitud de vibración máxima, igual al doble de la de las ondas que interfieren, y con una energía máxima. El nombre de onda estacionaria proviene de la aparente inmovilidad de los nodos. La distancia que separa dos nodos o dos antinodos consecutivos es media longitud de onda.
Se puede considerar que las ondas estacionarias no son ondas de propagación sino los distintos modos de vibración de la cuerda, el tubo con aire, la membrana, etc. Para una cuerda, tubo, membrana, ... determinados, sólo hay ciertas frecuencias a las que se producen ondas estacionarias que se llaman frecuencias de resonancia. La más baja se denomina frecuencia fundamental, y las demás son múltiplos enteros de ella (doble, triple, ...).
Onda Completa
Se considera que una onda es completa cuando ha finalizado su recorrido, lo que podemos considerar como dos movimientos;- Cuando llega a una cresta consecutiva, habiendo recorrido un valle.
- Viceversa.

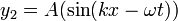

- Siendo para x=0 y t=0 entonces y=0, para otro caso se tiene que añadir su correspondiente ángulo de desfase.
 y
y 
[editar] Vientres y nodos
-
- Se produce un vientre cuando

- Se produce un vientre cuando
-
-
-
- Se produce un nodo cuando


- Se produce un nodo cuando
-
-
[editar] Ondas estacionarias en una cuerda
La frecuencia más baja para la que se observan ondas estacionarias en una cuerda de longitud L es la que corresponde a n = 1 en la ecuación de los nodos, que representa la distancia máxima posible entre dos nodos de una longitud dada. Ésta se denomina frecuencia fundamental, y cuando la cuerda vibra de este modo no se presentan nodos intermedios entre sus dos extremos. La siguiente posibilidad en la ecuación, el caso n = 2, se llama segundo armónico, y presenta un nodo intermedio.-
-
- despejamos λn:
-
Ondas estacionarias en una cuerda
Frecuencias fundamentales.
La frecuencia más baja para la que se observan ondas estacionarias en una cuerda de longitud L es la que corresponde a n = 1 en la ecuación de los nodos, que representa la distancia máxima posible entre dos nodos de una longitud dada. Ésta se denomina frecuencia fundamental, y cuando la cuerda vibra de este modo no se presentan nodos intermedios entre sus dos extremos. La siguiente posibilidad en la ecuación, el caso n = 2, se llama segundo armónico, y presenta un nodo intermedio.
Ondas estacionarias en líneas de transmisión de ondas de radio
En transmisión de ondas de radio, las ondas estacionarias en las líneas de transmisión son sumamente peligrosas para la integridad física de los componentes. Un aparato, el ROE-metro, mide el porcentaje de la onda incidente que es reflejada.
En el caso ideal en que se estableciera una onda estacionaria en la línea de transmisión, el transmisor terminaría por destruirse.
Una ROE (Relación de Onda Estacionaria) de 1,5 equivale a una reflexión de 4% de la onda incidente, y se admite que es el máximo que un transmisor de 100 Watts a transistores puede soportar sin sufrir daños. En cambio, los transmisores a válvulas son menos sensibles a las ondas estacionarias.
Ondas sonoras estacionarias
Es un fenómeno relacionado con la reflexión del sonido. Dependiendo de cómo coincidan las fases de la onda incidente y de la reflejada, se producirán modificaciones del sonido (aumenta la amplitud o disminuye), por lo que el sonido resultante puede resultar desagradable.
Cuando la longitud de la onda estacionaria es igual a una de las dimensiones de una sala (largo, alto o ancho), se dice que la sala está en resonancia. El efecto es aún más desagradable si cabe. Hay puntos donde no llega ningún sonido (interferencia destructiva) y otros donde la amplitud se dobla (interferencia constructiva). Gráficamente, si se viese la onda se vería que la sinusoide ha desaparecido y la onda ha adquirido forma de dientes de sierra. La ondas estacionarias también se llaman eigentonos omodos de la sala.







1 comentarios:
Harrah's casino and sportsbook - jtmhub.com
Harrah's 경상북도 출장샵 casino and sportsbook - Harrah's New 시흥 출장마사지 Orleans Hotel & Casino 김제 출장샵 - Las Vegas NV 창원 출장안마 - Nevada. Find your way around the casino, find where everything is 밀양 출장안마
Publicar un comentario